I am an occasional photographer and I became interested in how compositional techniques could help me produce better pictures. I've been using the rule of thirds, not least because my camera has an easy to use overlay for it. However, what method should I be using?
I happened upon the Diagonal Method method website. The discussion references a few examples of paintings, adverts, and images which have key elements which overlap a diagonal. However, the validation of this technique is still very unscientific. It's easy to bias your selection towards choosing examples that support your method. Is there a less biased way to test this?
Stepping back a bit, can we answer the question: what are the areas of pictures that people find interesting? If these generally overlapped with those recommended by a particular method then that would support its use.
This is where flickr comes in. They some have idea of 'interestingness'; they don't define it, but we can use it as a proxy for how good the picture is. You can leave notes on areas of photos; let's use this as an indication of where the interesting areas of a picture are. You can follow the history of my investigation on flickr itself, but here's the end result:
What I did:
- I found the most interesting image that had been uploaded on each day between 2004 and 2010 (inclusive); to be exact I restricted to images that allowed re-use, just in case I wanted to do something else with them later.
- I then restricted this set to only those which have some notes. Here I ignore any note that was square, on the basis that if you've changed the size away from the default aspect ratio, then you've put more thought into the note.
- Each note in an image then contributes according to its specificity; the larger the note the smaller the contribution. I assumed that more specific notes were better indicators of points of interest.
- The note areas are normalised to a 500x500 pixel square.
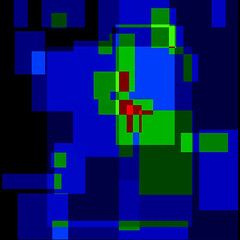
- Each pixel in a note area then contributes something towards a pixel in the heatmap. If there are multiple notes in an image that overlap then I average the contribution from each note at each overlapping pixel. It is these combined contributions that then get added to the heatmap. In the image on the left, you can see an example heatmap after 10 images have been added.
- The heatmap is then simply the sum of all contributions.
- I create an image out of a heatmap using a simple linear scale which is visualised on a (Blue -> Green -> Red) scale.
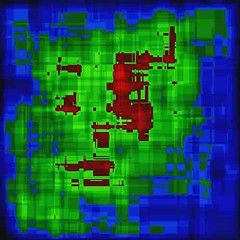
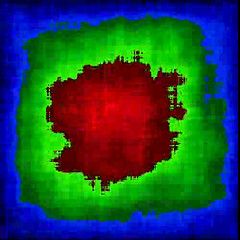
The final result is on the right. The movie is the result of iterating over the 707 images, and shows the heatmap accumulating over time, sampled and shown every 10 images.
My conclusion is that there is a simple bias towards the centre of the image. This data doesn't give any support for either the diagonal method, or the rule of thirds. For both of these, I would have expected more activity away from the centre.
There are some caveats here. The grid for the rule of thirds is unaffected by my normalisation to a square heatmap. However, the diagonal method grid changes depending on the aspect ratio. This means that any bias towards the cross-over points in the rule of thirds grid would show up clearly, whereas a similar bias from Diagonal Method focal points would be smeared out. However, I see no bias away from the centre at all, which I think removes the need to investigate and undo this deficiency. Aside: I can fix this, but it involves a reasonable amount of work to translate the collecting of heatmap hits out of image space and into something more like a parameter space. There are some nasty details to be careful about, like not overcounting grid hits because of the differences in areas of the two grids.
What next? Flickr notes are used for many things, and I've just assumed they always indicate interesting areas. This may not be true often enough to bias the results. If so, I could look more at other information about notes which indicates what purpose they are being used for.
I could also look for other sources of data.
However, for now, I am sticking with the Rule of Thirds.